| Главная » Статьи » Образовательные » Программирование |
Типы в функциональных языкахВ первой лекции говорилось, что аргументами функций могут быть не только переменные базовых типов, но и другие функции. В этом случае появляется понятие функции высшего порядка. Но для рассмотрения функций высшего порядка необходимо ввести понятие функционального типа (или тип функции). Пусть некоторая функция f — это функция одной переменной из множества A, принимающая значение из множества B. Тогда по определению:  Знак Например: Для функций многих аргументов определение типа можно выводить при помощи операции декартового произведения (например, В 1924 году М. Шёнфинкель предложил представлять функции многих аргументов как последовательность функций одного аргумента. В этом случае тип функции, которая складывает два действительных числа, выглядит так: Пример 8. Тип функции Предположительно, каждый из аргументов функции Для того чтобы не изощряться с написанием функций типа Таким образом, если функция f имеет тип Соответственно выражение, в котором все функции рассматриваются как функции одного аргумента, а единственной операцией является аппликация (применение), называются выражениями в форме «оператор-операнд». Такие функции получили название «каррированные», а сам процесс сведения типа функции к виду, приведённому в предыдущем абзаце — каррированием (по имени Карри Хаскелла). В λ-исчислении также присутствует математическая абстракция для аппликативных форм записей. Например:
И так далее. Несколько слов о нотации абстрактного языкаОбразцы и клозыНеобходимо отметить, что в нотации абстрактного функционального языка, который использовался до сих пор для написания примеров функций, можно было бы использовать такую конструкцию, как
Однако данная запись чревата непониманием и трудным разбором. Поэтому даже в примере 7 была использована нотация, которая поддерживает так называемые «образцы». Определение: Образцом называется выражение, построенное с помощью операций конструирования данных, которое используется для сопоставления с данными. Переменные обозначаются прописными буквами, константы — строчными. Примеры образцов:
К образцам предъявляется единственое требование, без которого сопоставление с образцами может быть выполнено неверно. Требование это звучит следующим образом: при сопоставлении образца с данными означивание переменных должно происходить единственным образом. То есть, например, выражение Кроме образцов в функциональном программировании вводится такое понятие, как «клоз» (от англ. «clause»). По определению клозы выглядят так:
где:
Таким образом, определение функции в функциональном программировании есть просто последовательность клозов (возможно состоящая из одного элемента). Для того, чтобы упростить запись определений функций, далее слово Пример 9. Образцы и клозы в функции
Пусть вызов функции Интерпретация вызова функции заключается в нахождении первого по порядку сверху вниз образца, успешно сопоставимого с фактическим параметром. Значение переменных образца, означиваемые в результате сопоставления, подставляются в правую часть клоза (выражение ОхранаПри написании функций в абстрактной нотации допустимо использовать так называемую охрану, то есть ограничения на значения переменных образца. Например, при использовании охраны функция
В рассмотренном коде слова́
Представленная запись не очень читабельна, поэтому использоваться она будет только в крайних случаях по необходимости. Локальные переменныеКак уже́ говорилось, использование локальных переменных представляет собой побочный эффект, поэтому оно недопустимо в функциональных языках. Однако в некоторых случаях использование локальных переменных носит оптимизирующий характер, что позволяет сэкономить время и ресурсы во время вычислений. Пусть f и h — функции, и необходимо вычислить выражение
(слова́ Элементы программированияНакапливающий параметр — аккумуляторБывает так, что при выполнении функции исключительно сёрьезно встаёт проблема расхода памяти. Эту проблему можно пояснить на примере функции, вычисляющей факториал числа:
Если провести пример вычисления этой функции с аргументом 3, то можно будет увидеть следующую последовательность:
==> ==> ==> ==> ==> ==> ==> 6 На примере этого вычисления наглядно видно, что при рекурсивных вызовах функций очень сильно используется память. В данном случае количество памяти пропорционально значению аргумента, но аргументов может быть большее число. Возникает резонный вопрос: можно ли так написать функцию вычисления факториала (и ей подобные), чтобы память использовалась минимально? Чтобы ответить на данный вопрос положительно, необходимо рассмотреть понятие аккумулятора (накопителя). Для этого можно рассмотреть следующий пример: Пример 10. Функция вычисления факториала с аккумулятором.
В этом примере второй параметр функции F выполняет роль аккумулирующей переменной, именно в ней содержится результат, который возвращается по окончании рекурсии. Сама же рекурсия в этом случае принимает вид «хвостовой», память при этом расходуется только на хранение адресов возврата значения функции. Хвостовая рекурсия представляет собой специальный вид рекурсии, в которой имеется единственный вызов рекурсивной функции и при этом этот вызов выполняется после всех вычислений. При реализации вычисления хвостовой рекурсии могут выполняться при помощи итераций в постоянном объёме памяти. На практике это обозначает, что «хороший» транслятор функционального языка должен «уметь» распознавать хвостовую рекурсию и реализовывать её в виде цикла. В свою очередь, метод накапливающего параметра не всегда приводит к хвостовой рекурсии, однако он однозначно помогает уменьшить общий объём памяти. Принципы построения определений с накапливающим параметром
Возникает вопрос: любую ли функцию можно преобразовать для вычисления с аккумулятором? Очевидно, что ответ на этот вопрос отрицателен. Построение функций с накапливающим параметром — приём не универсальный, и он не гарантирует получения хвостовой рекурсии. С другой стороны, построение определений с накапливающим параметром является делом творческим. В этом процессе необходимы некоторые эвристики. Определение: Общий вид рекурсивных определений, позволяющих при трансляции обеспечить вычисления в постоянном объёме памяти через итерацию, называется равенствами в итеративной форме. Общий вид равенств в итеративной форме может быть описан следующим образом: При этом на выражения eij накладываются следующие ограничения:
| |
| Просмотров: 1040 | Рейтинг: 0.0/0 |
| Всего комментариев: 0 | |






 обозначает «тип функции
обозначает «тип функции  , носят название функциональных типов. Иногда для их обозначения используется более изощрённая запись:
, носят название функциональных типов. Иногда для их обозначения используется более изощрённая запись:  ,
, 
 ). Однако в функциональном программировании такой способ определения типов функций многих переменных не прижился.
). Однако в функциональном программировании такой способ определения типов функций многих переменных не прижился. . То есть тип таких функций получается последовательным применением символа стрелки
. То есть тип таких функций получается последовательным применением символа стрелки  .
. уже́ означен, пусть
уже́ означен, пусть  , которая прибавляет к своему единственному аргументу число
, которая прибавляет к своему единственному аргументу число  . Теперь, возвращаясь назад, можно понять, почему тип функции
. Теперь, возвращаясь назад, можно понять, почему тип функции  , а когда аргументы получают конкретные значения (например,
, а когда аргументы получают конкретные значения (например,  , сначала вычисляются все функции, пока не появится функция одного аргумента, которая применяется к последнему.
, сначала вычисляются все функции, пока не появится функция одного аргумента, которая применяется к последнему. , то чтобы полностью вычислить значение
, то чтобы полностью вычислить значение  необходимо последовательно провести вычисление
необходимо последовательно провести вычисление  . И результатом вычисления будет объект типа
. И результатом вычисления будет объект типа 
 . Например, при описании функции
. Например, при описании функции  , её тело можно было бы записать следующим образом:
, её тело можно было бы записать следующим образом:![\operatorname{append}(L_1, L_2) = \operatorname{if} (L_1 = [\,])\ \operatorname{then}\ L_2\ \operatorname{else}\ \operatorname{head}(L_1) : \operatorname{append}(\operatorname{tail}(L_1), L_2)](http://upload.wikimedia.org/wikibooks/ru/math/7/0/3/7037a73355ebe4fc537edc3b0c7e7a74.png)
 можно использовать как образец, так как означивание переменной
можно использовать как образец, так как означивание переменной  использовать в качестве образца нельзя, ибо означить переменные
использовать в качестве образца нельзя, ибо означить переменные
 и
и  );
); — выражение.
— выражение. .
.![\operatorname{length}([\,]) = 0](http://upload.wikimedia.org/wikibooks/ru/math/5/3/0/53071d42922c115168eb80835642b7ba.png)

![\operatorname{length}(L) = 0\ \mathbf{when}\ L = [\,]](http://upload.wikimedia.org/wikibooks/ru/math/5/7/2/572ed29d0706c64f439ebae253b0ab87.png)

 (когда) и
(когда) и  (в противном случае) являются зарезервированными словами языка. Однако использование этих слов не является необходимым условием для организации охраны. Охрану можно организовывать различными способами, в том числе и с помощью λ-исчисления:
(в противном случае) являются зарезервированными словами языка. Однако использование этих слов не является необходимым условием для организации охраны. Охрану можно организовывать различными способами, в том числе и с помощью λ-исчисления:![\operatorname{append} = \lambda [\,].(\lambda L.L)](http://upload.wikimedia.org/wikibooks/ru/math/4/0/c/40cbd30e33bc38d5ad02a8530346fe58.png)

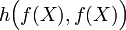 . Если в языке нет оптимизирующих методов, то в этом случае произойдёт двойное вычисление выражения
. Если в языке нет оптимизирующих методов, то в этом случае произойдёт двойное вычисление выражения  . Естественно, что в этом случае выражение
. Естественно, что в этом случае выражение 
 ,
,  — зарезервированы в языке). В этом случае переменная
— зарезервированы в языке). В этом случае переменная 











